华联于 2012 年 7 月~ 9 月的科技专题中,介绍芯片实验设计时,概略介绍了一些常用的数据分析方法,有许多客户及好学的读者纷纷来信,希望我们另辟单元,仔细教学这些对他们很有帮助的分析软件;数据分析素来是华联的强项之一,我们很乐意也很兴奋地开辟这个新单元 - 数据分析教学,本期以主成份分析法 (Principal Component Analysis,PCA)作为起头,并搭配影片教学,让大家学习事半功倍。
在微阵列数据 (Microarray data) 分析中,主成份分析法 (PCA) 是一种常用于简化数据集 (Data set)、观察样本或基因群之间相关性的技术。微阵列数据通常是上万笔基因、数十个样本所组成的一个数据矩阵,利用主成份分析可以减少数据的维数 (Dimension),同时保留数据对变异数贡献最大的特征,藉以观察样本或基因群的主要差异。主要原理是经由保留低阶主成分,并忽略高阶主成分。通常低阶成分较能够保留住数据的最重要成分。但是由于主成份分析依赖所给予的数据,所以数据的准确性(或者我们也可以说实验的准确与否)对分析结果影响很大。
主成份分析法由卡尔.皮尔逊于1901年创建,用于分析数据及建立数理模型。其方法主要是通过对共变异数矩阵(这边可以想成微阵列数据矩阵)进行特征分解3,以得出数据的主成份(即特征向量, Eigenvector) 与它们的权值(或称特征值, Eigenvalue) 。特征向量的长度在该线性变换下缩放的比例我们称之为其特征值,前面提到,将影响样本变异数贡献最大的特征向量放于第一维度,第二贡献度的放于第二维度,藉此可得到样本于平面坐标之间的关系图,如图一。

这边我们用颜色来区分不同样本,微阵列实验常以技术性重复来增加统计上的意义,图中技术性重复以同一颜色来表示。一般来说,技术性重复的实验因为来自同一管制备的RNA,所以理论上相关性应该很高;但由于样本取得、实验过程、数据取得以及分析方式都可能造成误差,所以实际上的结果会有变异性。图中可见到技术性重复的结果很接近,但是标示黑色、紫色的样本和红色、绿色样本间”特征差异性”比较大。我们也可以利用前三组贡献最大的特征向量画成3 度空间分布图(如图二),能进一步了解样本于空间中分布的情形;从图中可以发现,当我们转了一个角度,标示红色和绿色的样本在空间坐标中还是有段距离;代表其特征值还是有差异性。
数据对应的特征值如表一,我们可以观察到这边将主成份 (Principal Components) 分成PC1~PC7共七等份,全部加成起来代表了所有样本的特征信息,以百分比 (%Var)表示的话,总共100%;用白话一点的方式来说,前三个主成份(维度)就可以取得这些样本约略 84%的特征信息,足以用其代表的特征值来区分样本之间的差异性。所以当实验完成、取得微阵列数据后,常常第一件事就是做主成份分析或丛集式分群分析(HierarchicalClustering),观察样本间的技术性或生物性重复做的好不好、实验组和对照组之间的差异大不大,以及是否可以观察到样本间的特征差异性等等。这样的分析可以做为一种质量控管(Quality Control)的依据,决定是否继续分析或是重新作实验的重要参考指标。
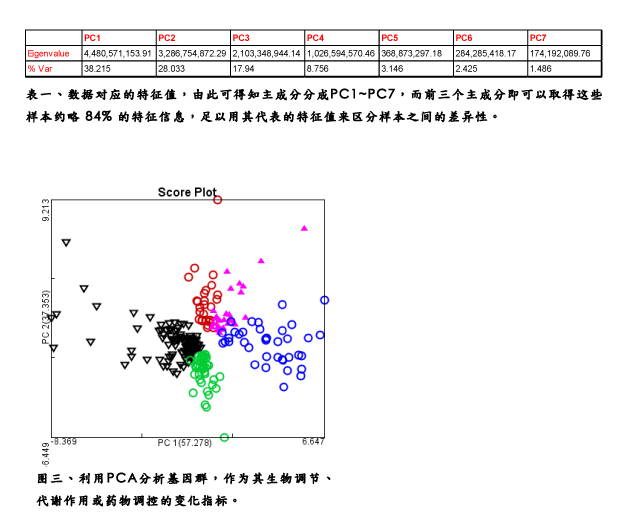
之后的分析工作,主成份分析也扮演了重要角色。特别当我们找出一些基因群、足以分别代表其生物调节功能、代谢作用或药物调控的变化指标,也可以将这些基因作主成份分析,如图三。这边我们特定挑选了一些有显著差异表现的基因来试作,经过主成份分析后被分成了五群,每个颜色代表一特定基因群,而每个基因群在研究中可能扮演了重要的调控机制。
小结
本期介绍的主成份分析为芯片数据分析的第一关,将芯片数万点的信息简化成几个低维度的分析数据,以归纳出彼此的群落分布,藉以比对各自的近似关系;观察样本间的技术性或生物性重复做的好不好、可不可信,进而决定是否继续接下来的进阶分析。
华联将在未来几期的科技专题中介绍更多的数据分析方法,包含丛集式分群分析(Hierarchical Clustering)、基因功能分类 (Gene Ontology)、讯息传递路径分析 (Pathways analysis)...等等,若有分析上的疑惑也欢迎随时与我们连络哟!。
更多有关华联产品,请访问 www.onearray.com.cn
